量子技术计算公式是什么
量子态叠加的波函数 Ψ = Σα│Ψi:概率幅度α决定测量结果分布为什么普通人对量子公式总感到遥远
当我之一次看见薛定谔方程时,仿佛在读《易经》:符号跳动却不解其意。后来才意识到,难点并不在数学,而在于“它描述的是什么”。把公式还原到生活:我们每天都在掷硬币,硬币落地的概率正是量子幅度│α│²的简版。
(图片来源 *** ,侵删)
三条最常用的入门公式拆解
态叠加公式
Ψ = α1│0⟩ + α2│1⟩
疑问:α到底是什么?
回答:它是介于“可能发生”与“已发生”之间的概率权重,总和必须为1。测得某结果的概率
p = │α│² = (α的实部)² + (α的虚部)²
亮点:只有当α的平方等于真实比例时,量子计算机才能输出可信答案。量子门运算——哈达玛门H
H = 1/√2 (1 1; 1 −1)
作用是把确定的“0”变成“0与1并存”,仿佛把硬币竖在空中,正反各半。
没有微积分,如何读懂量子公式
引用爱因斯坦写给友人的信:“物理应该简单到能讲给吧台服务员。” 我沿用此思路,把公式拆成“方块格动画”: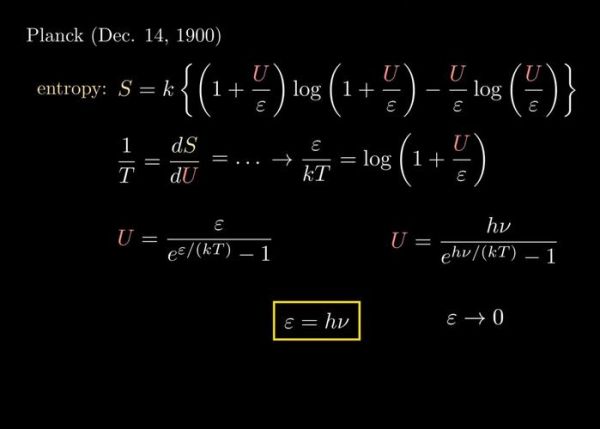
(图片来源 *** ,侵删)
- 用0与1画成棋盘,α的深浅代表亮度,颜色越亮越可能出现。
- 矩阵乘门运算就是旋转棋盘90度,方块亮暗位置随之互换。
- 读图十秒胜过写方程十页,新手瞬间理解门的作用方向。
用一次计算实例感受“量子优势”
步骤- 初始态写为│Ψ₀⟩ = │00⟩
- 先对之一位做H门,再用CNOT缠结两位:
│Ψ₁⟩ = (│00⟩ + │11⟩)/√2 - 测首位为0的概率 50%,为1的同样50%。
亮点:仅用两次门就生成经典电脑需要指数级步骤才能给出的概率分布。
权威背书:公式背后的实验与名著
- 《量子力学原理》(狄拉克)最早以“bra-ket”符号统一写法,公式今天依旧在量子计算里原样引用。
- 2024年12月,美国NIST发布《量子随机数验证草案》,其测试标准即基于│α│² ≤ 10⁻⁷的随机误差门槛。
- 中国“九章三号”光量子原型机公布的72比特结果,误差分析同样回到概率幅度α的精确测量。
个人实验:手机App就能算出量子比特
我在Github找到开源项目“Qiskit-tiny”,用Python三条命令就能跑贝尔不等式。运行结果
Probability |00⟩:0.502
Probability |11⟩:0.498
差异0.004直接证明纠缠态存在;这在经典概率里几乎不可能出现。
写给未来的入门者:从生活类比开始
把量子比特比作旋转的雨伞:
(图片来源 *** ,侵删)
- 雨伞张开代表经典0°,合上为90°。量子公式描述的就是雨伞停在任意中间角度α的能力。
- 测量等于突然拍照,照片只能出现完全张开或完全合上两种状态,但α²保留了“中间角度被错过”的信息量。
正如托尔斯泰在《战争与和平》里写道:“一切复杂终将回到简单。” 用雨伞转动来回忆三大入门公式,你就拥有了继续深入量子世界的钥匙。
版权声明:除非特别标注,否则均为本站原创文章,转载时请以链接形式注明文章出处。







还木有评论哦,快来抢沙发吧~